diff --git a/src/main/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/Solution.java b/src/main/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/Solution.java
new file mode 100644
index 000000000..b6b97952a
--- /dev/null
+++ b/src/main/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/Solution.java
@@ -0,0 +1,15 @@
+package g3401_3500.s3423_maximum_difference_between_adjacent_elements_in_a_circular_array;
+
+// #Easy #Array #2025_01_22_Time_1_(99.86%)_Space_43.72_(36.06%)
+
+public class Solution {
+ public int maxAdjacentDistance(int[] nums) {
+ int maxDiff = 0;
+ for (int i = 0; i < nums.length; i++) {
+ int nextIndex = (i + 1) % nums.length;
+ int diff = Math.abs(nums[i] - nums[nextIndex]);
+ maxDiff = Math.max(maxDiff, diff);
+ }
+ return maxDiff;
+ }
+}
diff --git a/src/main/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/readme.md b/src/main/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/readme.md
new file mode 100644
index 000000000..924b26986
--- /dev/null
+++ b/src/main/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/readme.md
@@ -0,0 +1,32 @@
+3423\. Maximum Difference Between Adjacent Elements in a Circular Array
+
+Easy
+
+Given a **circular** array `nums`, find the **maximum** absolute difference between adjacent elements.
+
+**Note**: In a circular array, the first and last elements are adjacent.
+
+**Example 1:**
+
+**Input:** nums = [1,2,4]
+
+**Output:** 3
+
+**Explanation:**
+
+Because `nums` is circular, `nums[0]` and `nums[2]` are adjacent. They have the maximum absolute difference of `|4 - 1| = 3`.
+
+**Example 2:**
+
+**Input:** nums = [-5,-10,-5]
+
+**Output:** 5
+
+**Explanation:**
+
+The adjacent elements `nums[0]` and `nums[1]` have the maximum absolute difference of `|-5 - (-10)| = 5`.
+
+**Constraints:**
+
+* `2 <= nums.length <= 100`
+* `-100 <= nums[i] <= 100`
\ No newline at end of file
diff --git a/src/main/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/Solution.java b/src/main/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/Solution.java
new file mode 100644
index 000000000..794d94979
--- /dev/null
+++ b/src/main/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/Solution.java
@@ -0,0 +1,21 @@
+package g3401_3500.s3424_minimum_cost_to_make_arrays_identical;
+
+// #Medium #Array #Sorting #Greedy #2025_01_22_Time_60_(98.08%)_Space_57.68_(39.04%)
+
+import java.util.Arrays;
+
+public class Solution {
+ public long minCost(int[] arr, int[] brr, long k) {
+ long res1 = 0;
+ long res2 = 0;
+ for (int i = 0; i < arr.length; ++i) {
+ res1 += Math.abs(arr[i] - brr[i]);
+ }
+ Arrays.sort(arr);
+ Arrays.sort(brr);
+ for (int i = 0; i < arr.length; ++i) {
+ res2 += Math.abs(arr[i] - brr[i]);
+ }
+ return Math.min(res1, res2 + k);
+ }
+}
diff --git a/src/main/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/readme.md b/src/main/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/readme.md
new file mode 100644
index 000000000..2cd554df5
--- /dev/null
+++ b/src/main/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/readme.md
@@ -0,0 +1,43 @@
+3424\. Minimum Cost to Make Arrays Identical
+
+Medium
+
+You are given two integer arrays `arr` and `brr` of length `n`, and an integer `k`. You can perform the following operations on `arr` _any_ number of times:
+
+* Split `arr` into _any_ number of **contiguous** **non-empty subarrays** and rearrange these subarrays in _any order_. This operation has a fixed cost of `k`.
+* Choose any element in `arr` and add or subtract a positive integer `x` to it. The cost of this operation is `x`.
+
+
+Return the **minimum** total cost to make `arr` **equal** to `brr`.
+
+**Example 1:**
+
+**Input:** arr = [-7,9,5], brr = [7,-2,-5], k = 2
+
+**Output:** 13
+
+**Explanation:**
+
+* Split `arr` into two contiguous subarrays: `[-7]` and `[9, 5]` and rearrange them as `[9, 5, -7]`, with a cost of 2.
+* Subtract 2 from element `arr[0]`. The array becomes `[7, 5, -7]`. The cost of this operation is 2.
+* Subtract 7 from element `arr[1]`. The array becomes `[7, -2, -7]`. The cost of this operation is 7.
+* Add 2 to element `arr[2]`. The array becomes `[7, -2, -5]`. The cost of this operation is 2.
+
+The total cost to make the arrays equal is `2 + 2 + 7 + 2 = 13`.
+
+**Example 2:**
+
+**Input:** arr = [2,1], brr = [2,1], k = 0
+
+**Output:** 0
+
+**Explanation:**
+
+Since the arrays are already equal, no operations are needed, and the total cost is 0.
+
+**Constraints:**
+
+* 1 <= arr.length == brr.length <= 105
+* 0 <= k <= 2 * 1010
+* -105 <= arr[i] <= 105
+* -105 <= brr[i] <= 105
\ No newline at end of file
diff --git a/src/main/java/g3401_3500/s3425_longest_special_path/Solution.java b/src/main/java/g3401_3500/s3425_longest_special_path/Solution.java
new file mode 100644
index 000000000..1be9ee2aa
--- /dev/null
+++ b/src/main/java/g3401_3500/s3425_longest_special_path/Solution.java
@@ -0,0 +1,96 @@
+package g3401_3500.s3425_longest_special_path;
+
+// #Hard #Array #Hash_Table #Depth_First_Search #Tree #Sliding_Window
+// #2025_01_22_Time_49_(74.66%)_Space_98.04_(44.26%)
+
+import java.util.ArrayList;
+import java.util.Arrays;
+
+@SuppressWarnings("unchecked")
+public class Solution {
+ private ArrayList[] adj;
+ private int[] nums;
+ private int[] dist;
+ private int[] lastOccur;
+ private ArrayList pathStack;
+ private int minIndex;
+ private int maxLen;
+ private int minNodesForMaxLen;
+
+ public int[] longestSpecialPath(int[][] edges, int[] nums) {
+ int n = nums.length;
+ this.nums = nums;
+ adj = new ArrayList[n];
+ for (int i = 0; i < n; i++) {
+ adj[i] = new ArrayList<>();
+ }
+ for (int[] e : edges) {
+ int u = e[0];
+ int v = e[1];
+ int w = e[2];
+ adj[u].add(new int[] {v, w});
+ adj[v].add(new int[] {u, w});
+ }
+ dist = new int[n];
+ buildDist(0, -1, 0);
+ int maxVal = 0;
+ for (int val : nums) {
+ if (val > maxVal) {
+ maxVal = val;
+ }
+ }
+ lastOccur = new int[maxVal + 1];
+ Arrays.fill(lastOccur, -1);
+ pathStack = new ArrayList<>();
+ minIndex = 0;
+ maxLen = 0;
+ minNodesForMaxLen = Integer.MAX_VALUE;
+ dfs(0, -1);
+ return new int[] {maxLen, minNodesForMaxLen};
+ }
+
+ private void buildDist(int u, int parent, int currDist) {
+ dist[u] = currDist;
+ for (int[] edge : adj[u]) {
+ int v = edge[0];
+ int w = edge[1];
+ if (v == parent) {
+ continue;
+ }
+ buildDist(v, u, currDist + w);
+ }
+ }
+
+ private void dfs(int u, int parent) {
+ int stackPos = pathStack.size();
+ pathStack.add(u);
+ int val = nums[u];
+ int oldPos = lastOccur[val];
+ int oldMinIndex = minIndex;
+ lastOccur[val] = stackPos;
+ if (oldPos >= minIndex) {
+ minIndex = oldPos + 1;
+ }
+ if (minIndex <= stackPos) {
+ int ancestor = pathStack.get(minIndex);
+ int pathLength = dist[u] - dist[ancestor];
+ int pathNodes = stackPos - minIndex + 1;
+ if (pathLength > maxLen) {
+ maxLen = pathLength;
+ minNodesForMaxLen = pathNodes;
+ } else if (pathLength == maxLen && pathNodes < minNodesForMaxLen) {
+ minNodesForMaxLen = pathNodes;
+ }
+ }
+ for (int[] edge : adj[u]) {
+ int v = edge[0];
+ if (v == parent) {
+ continue;
+ }
+ dfs(v, u);
+ }
+ pathStack.remove(pathStack.size() - 1);
+ lastOccur[val] = oldPos;
+ minIndex = oldMinIndex;
+ }
+}
diff --git a/src/main/java/g3401_3500/s3425_longest_special_path/readme.md b/src/main/java/g3401_3500/s3425_longest_special_path/readme.md
new file mode 100644
index 000000000..53b174799
--- /dev/null
+++ b/src/main/java/g3401_3500/s3425_longest_special_path/readme.md
@@ -0,0 +1,48 @@
+3425\. Longest Special Path
+
+Hard
+
+You are given an undirected tree rooted at node `0` with `n` nodes numbered from `0` to `n - 1`, represented by a 2D array `edges` of length `n - 1`, where edges[i] = [ui, vi, lengthi] indicates an edge between nodes ui and vi with length lengthi. You are also given an integer array `nums`, where `nums[i]` represents the value at node `i`.
+
+A **special path** is defined as a **downward** path from an ancestor node to a descendant node such that all the values of the nodes in that path are **unique**.
+
+**Note** that a path may start and end at the same node.
+
+Return an array `result` of size 2, where `result[0]` is the **length** of the **longest** special path, and `result[1]` is the **minimum** number of nodes in all _possible_ **longest** special paths.
+
+**Example 1:**
+
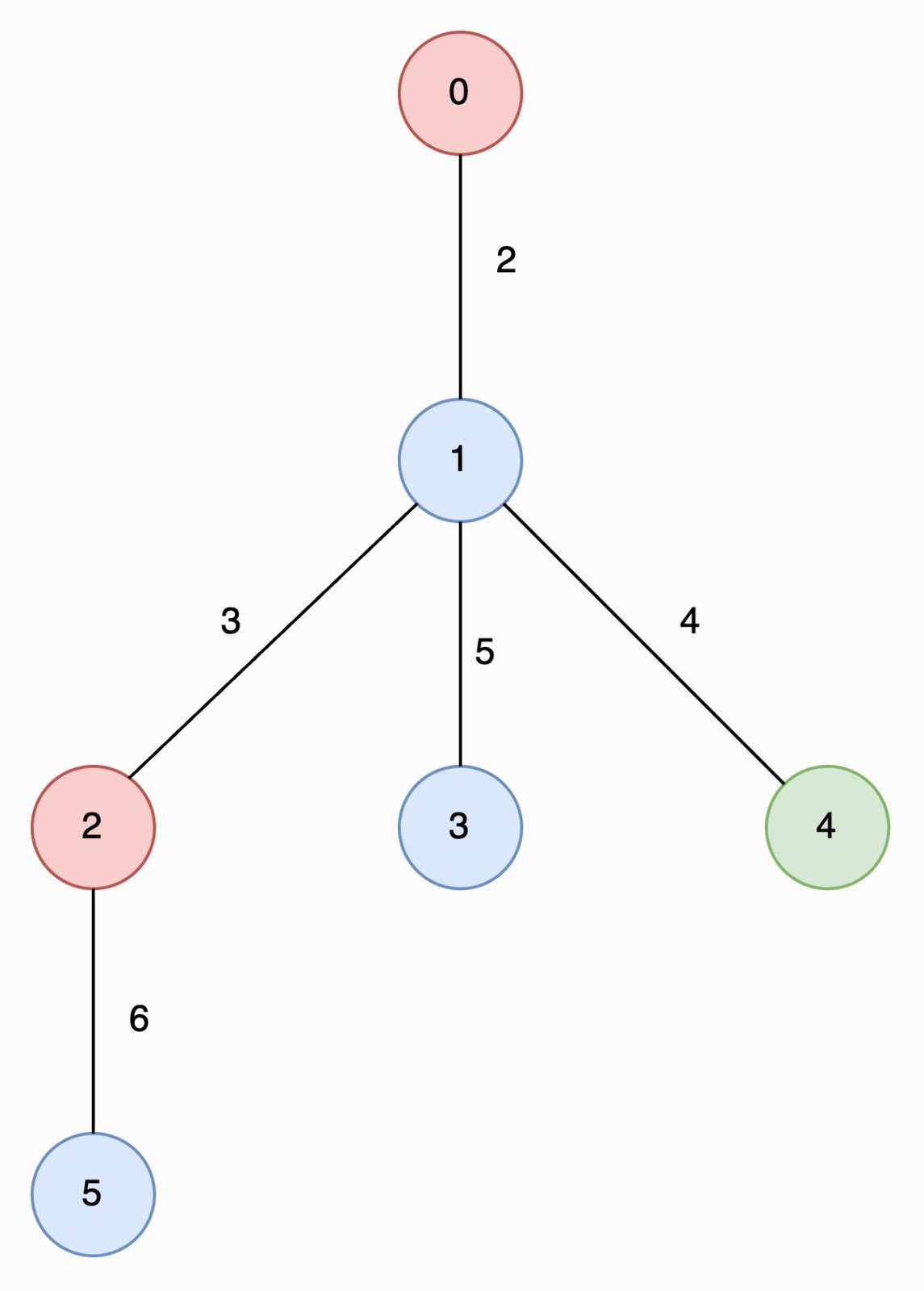
+**Input:** edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], nums = [2,1,2,1,3,1]
+
+**Output:** [6,2]
+
+**Explanation:**
+
+#### In the image below, nodes are colored by their corresponding values in `nums`
+
+
+
+The longest special paths are `2 -> 5` and `0 -> 1 -> 4`, both having a length of 6. The minimum number of nodes across all longest special paths is 2.
+
+**Example 2:**
+
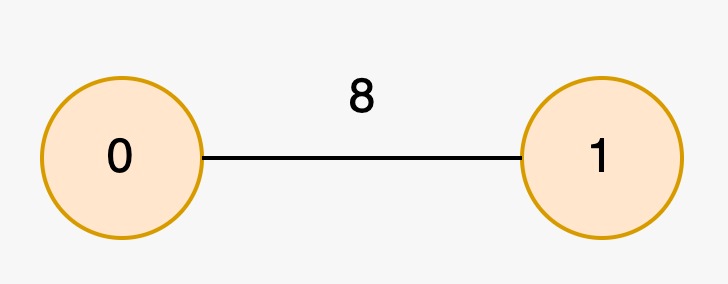
+**Input:** edges = [[1,0,8]], nums = [2,2]
+
+**Output:** [0,1]
+
+**Explanation:**
+
+
+
+The longest special paths are `0` and `1`, both having a length of 0. The minimum number of nodes across all longest special paths is 1.
+
+**Constraints:**
+
+* 2 <= n <= 5 * 104
+* `edges.length == n - 1`
+* `edges[i].length == 3`
+* 0 <= ui, vi < n
+* 1 <= lengthi <= 103
+* `nums.length == n`
+* 0 <= nums[i] <= 5 * 104
+* The input is generated such that `edges` represents a valid tree.
\ No newline at end of file
diff --git a/src/main/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/Solution.java b/src/main/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/Solution.java
new file mode 100644
index 000000000..7016aa07f
--- /dev/null
+++ b/src/main/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/Solution.java
@@ -0,0 +1,40 @@
+package g3401_3500.s3426_manhattan_distances_of_all_arrangements_of_pieces;
+
+// #Hard #Math #Combinatorics #2025_01_22_Time_20_(87.92%)_Space_40.82_(98.07%)
+
+public class Solution {
+ private long comb(long a, long b, long mod) {
+ if (b > a) {
+ return 0;
+ }
+ long numer = 1;
+ long denom = 1;
+ for (long i = 0; i < b; ++i) {
+ numer = numer * (a - i) % mod;
+ denom = denom * (i + 1) % mod;
+ }
+ long denomInv = 1;
+ long exp = mod - 2;
+ while (exp > 0) {
+ if (exp % 2 > 0) {
+ denomInv = denomInv * denom % mod;
+ }
+ denom = denom * denom % mod;
+ exp /= 2;
+ }
+ return numer * denomInv % mod;
+ }
+
+ public int distanceSum(int m, int n, int k) {
+ long res = 0;
+ long mod = 1000000007;
+ long base = comb((long) m * n - 2, k - 2L, mod);
+ for (int d = 1; d < n; ++d) {
+ res = (res + (long) d * (n - d) % mod * m % mod * m % mod) % mod;
+ }
+ for (int d = 1; d < m; ++d) {
+ res = (res + (long) d * (m - d) % mod * n % mod * n % mod) % mod;
+ }
+ return (int) (res * base % mod);
+ }
+}
diff --git a/src/main/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/readme.md b/src/main/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/readme.md
new file mode 100644
index 000000000..4e262e62c
--- /dev/null
+++ b/src/main/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/readme.md
@@ -0,0 +1,53 @@
+3426\. Manhattan Distances of All Arrangements of Pieces
+
+Hard
+
+You are given three integers `m`, `n`, and `k`.
+
+There is a rectangular grid of size `m × n` containing `k` identical pieces. Return the sum of Manhattan distances between every pair of pieces over all **valid arrangements** of pieces.
+
+A **valid arrangement** is a placement of all `k` pieces on the grid with **at most** one piece per cell.
+
+Since the answer may be very large, return it **modulo** 109 + 7.
+
+The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi - xj| + |yi - yj|.
+
+**Example 1:**
+
+**Input:** m = 2, n = 2, k = 2
+
+**Output:** 8
+
+**Explanation:**
+
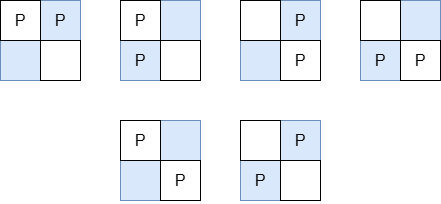
+The valid arrangements of pieces on the board are:
+
+
+
+* In the first 4 arrangements, the Manhattan distance between the two pieces is 1.
+* In the last 2 arrangements, the Manhattan distance between the two pieces is 2.
+
+Thus, the total Manhattan distance across all valid arrangements is `1 + 1 + 1 + 1 + 2 + 2 = 8`.
+
+**Example 2:**
+
+**Input:** m = 1, n = 4, k = 3
+
+**Output:** 20
+
+**Explanation:**
+
+The valid arrangements of pieces on the board are:
+
+
+
+* The first and last arrangements have a total Manhattan distance of `1 + 1 + 2 = 4`.
+* The middle two arrangements have a total Manhattan distance of `1 + 2 + 3 = 6`.
+
+The total Manhattan distance between all pairs of pieces across all arrangements is `4 + 6 + 6 + 4 = 20`.
+
+**Constraints:**
+
+* 1 <= m, n <= 105
+* 2 <= m * n <= 105
+* `2 <= k <= m * n`
\ No newline at end of file
diff --git a/src/main/java/g3401_3500/s3427_sum_of_variable_length_subarrays/Solution.java b/src/main/java/g3401_3500/s3427_sum_of_variable_length_subarrays/Solution.java
new file mode 100644
index 000000000..c713e549d
--- /dev/null
+++ b/src/main/java/g3401_3500/s3427_sum_of_variable_length_subarrays/Solution.java
@@ -0,0 +1,15 @@
+package g3401_3500.s3427_sum_of_variable_length_subarrays;
+
+// #Easy #Array #Prefix_Sum #2025_01_22_Time_0_(100.00%)_Space_43.77_(58.41%)
+
+public class Solution {
+ public int subarraySum(int[] nums) {
+ int res = nums[0];
+ for (int i = 1; i < nums.length; i++) {
+ int j = i - nums[i] - 1;
+ nums[i] += nums[i - 1];
+ res += nums[i] - (j < 0 ? 0 : nums[j]);
+ }
+ return res;
+ }
+}
diff --git a/src/main/java/g3401_3500/s3427_sum_of_variable_length_subarrays/readme.md b/src/main/java/g3401_3500/s3427_sum_of_variable_length_subarrays/readme.md
new file mode 100644
index 000000000..a3d7f6d72
--- /dev/null
+++ b/src/main/java/g3401_3500/s3427_sum_of_variable_length_subarrays/readme.md
@@ -0,0 +1,50 @@
+3427\. Sum of Variable Length Subarrays
+
+Easy
+
+You are given an integer array `nums` of size `n`. For **each** index `i` where `0 <= i < n`, define a **non-empty subarrays** `nums[start ... i]` where `start = max(0, i - nums[i])`.
+
+Return the total sum of all elements from the subarray defined for each index in the array.
+
+**Example 1:**
+
+**Input:** nums = [2,3,1]
+
+**Output:** 11
+
+**Explanation:**
+
+| i | Subarray | Sum |
+|-----|------------------------------|-----|
+| 0 | `nums[0] = [2]` | 2 |
+| 1 | `nums[0 ... 1] = [2, 3]` | 5 |
+| 2 | `nums[1 ... 2] = [3, 1]` | 4 |
+| **Total Sum** | | 11 |
+
+The total sum is 11. Hence, 11 is the output.
+
+**Example 2:**
+
+**Input:** nums = [3,1,1,2]
+
+**Output:** 13
+
+**Explanation:**
+
+Here's the HTML table converted to Markdown:
+
+| i | Subarray | Sum |
+|-----|------------------------------|-----|
+| 0 | `nums[0] = [3]` | 3 |
+| 1 | `nums[0 ... 1] = [3, 1]` | 4 |
+| 2 | `nums[1 ... 2] = [1, 1]` | 2 |
+| 3 | `nums[1 ... 3] = [1, 1, 2]` | 4 |
+| **Total Sum** | | 13 |
+
+This Markdown table replicates the structure and content of the original HTML table.
+The total sum is 13. Hence, 13 is the output.
+
+**Constraints:**
+
+* `1 <= n == nums.length <= 100`
+* `1 <= nums[i] <= 1000`
\ No newline at end of file
diff --git a/src/main/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/Solution.java b/src/main/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/Solution.java
new file mode 100644
index 000000000..6875b956b
--- /dev/null
+++ b/src/main/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/Solution.java
@@ -0,0 +1,64 @@
+package g3401_3500.s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences;
+
+// #Medium #Array #Dynamic_Programming #Math #Sorting #Combinatorics
+// #2025_01_22_Time_28_(99.74%)_Space_65.01_(35.71%)
+
+import java.util.Arrays;
+
+public class Solution {
+ private static final int MOD = (int) 1e9 + 7;
+ private long[] fact;
+ private long[] invFact;
+
+ public int minMaxSums(int[] nums, int k) {
+ int n = nums.length;
+ Arrays.sort(nums);
+ if (fact == null || fact.length < n + 1) {
+ buildFactorials(n);
+ }
+ long[] sum = new long[n + 1];
+ sum[0] = 1;
+ for (int i = 0; i < n; i++) {
+ long val = (2L * sum[i]) % MOD;
+ if (i + 1 >= k) {
+ val = (val - comb(i, k - 1) + MOD) % MOD;
+ }
+ sum[i + 1] = val;
+ }
+ long res = 0;
+ for (int i = 0; i < n; i++) {
+ long add = (sum[i] + sum[n - 1 - i]) % MOD;
+ res = (res + (nums[i] % MOD) * add) % MOD;
+ }
+ return (int) res;
+ }
+
+ private void buildFactorials(int n) {
+ fact = new long[n + 1];
+ invFact = new long[n + 1];
+ fact[0] = 1;
+ for (int i = 1; i <= n; i++) {
+ fact[i] = (fact[i - 1] * i) % MOD;
+ }
+ invFact[n] = pow(fact[n], MOD - 2);
+ for (int i = n - 1; i >= 0; i--) {
+ invFact[i] = (invFact[i + 1] * (i + 1)) % MOD;
+ }
+ }
+
+ private long comb(int n, int r) {
+ return fact[n] * invFact[r] % MOD * invFact[n - r] % MOD;
+ }
+
+ private long pow(long base, int exp) {
+ long ans = 1L;
+ while (exp > 0) {
+ if ((exp & 1) == 1) {
+ ans = (ans * base) % MOD;
+ }
+ base = (base * base) % MOD;
+ exp >>= 1;
+ }
+ return ans;
+ }
+}
diff --git a/src/main/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/readme.md b/src/main/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/readme.md
new file mode 100644
index 000000000..83f0095da
--- /dev/null
+++ b/src/main/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/readme.md
@@ -0,0 +1,59 @@
+3428\. Maximum and Minimum Sums of at Most Size K Subsequences
+
+Medium
+
+You are given an integer array `nums` and a positive integer `k`. Return the sum of the **maximum** and **minimum** elements of all
+
+**subsequences**
+
+of `nums` with **at most** `k` elements.
+
+Since the answer may be very large, return it **modulo** 109 + 7.
+
+**Example 1:**
+
+**Input:** nums = [1,2,3], k = 2
+
+**Output:** 24
+
+**Explanation:**
+
+The subsequences of `nums` with at most 2 elements are:
+
+| **Subsequence** | Minimum | Maximum | Sum |
+|-----------------|---------|---------|------|
+| `[1]` | 1 | 1 | 2 |
+| `[2]` | 2 | 2 | 4 |
+| `[3]` | 3 | 3 | 6 |
+| `[1, 2]` | 1 | 2 | 3 |
+| `[1, 3]` | 1 | 3 | 4 |
+| `[2, 3]` | 2 | 3 | 5 |
+| **Final Total** | | | 24 |
+
+The output would be 24.
+
+**Example 2:**
+
+**Input:** nums = [5,0,6], k = 1
+
+**Output:** 22
+
+**Explanation:**
+
+For subsequences with exactly 1 element, the minimum and maximum values are the element itself. Therefore, the total is `5 + 5 + 0 + 0 + 6 + 6 = 22`.
+
+**Example 3:**
+
+**Input:** nums = [1,1,1], k = 2
+
+**Output:** 12
+
+**Explanation:**
+
+The subsequences `[1, 1]` and `[1]` each appear 3 times. For all of them, the minimum and maximum are both 1. Thus, the total is 12.
+
+**Constraints:**
+
+* 1 <= nums.length <= 105
+* 0 <= nums[i] <= 109
+* `1 <= k <= min(70, nums.length)`
\ No newline at end of file
diff --git a/src/main/java/g3401_3500/s3429_paint_house_iv/Solution.java b/src/main/java/g3401_3500/s3429_paint_house_iv/Solution.java
new file mode 100644
index 000000000..596ca0701
--- /dev/null
+++ b/src/main/java/g3401_3500/s3429_paint_house_iv/Solution.java
@@ -0,0 +1,33 @@
+package g3401_3500.s3429_paint_house_iv;
+
+// #Medium #Array #Dynamic_Programming #2025_01_22_Time_5_(100.00%)_Space_106.29_(78.64%)
+
+public class Solution {
+ public long minCost(int n, int[][] cost) {
+ long dp0 = 0;
+ long dp1 = 0;
+ long dp2 = 0;
+ long dp3 = 0;
+ long dp4 = 0;
+ long dp5 = 0;
+ for (int i = 0; i < n / 2; ++i) {
+ long nextdp0 = Math.min(Math.min(dp2, dp3), dp4) + cost[i][0] + cost[n - i - 1][1];
+ long nextdp1 = Math.min(Math.min(dp2, dp4), dp5) + cost[i][0] + cost[n - i - 1][2];
+ long nextdp2 = Math.min(Math.min(dp0, dp1), dp5) + cost[i][1] + cost[n - i - 1][0];
+ long nextdp3 = Math.min(Math.min(dp0, dp4), dp5) + cost[i][1] + cost[n - i - 1][2];
+ long nextdp4 = Math.min(Math.min(dp0, dp1), dp3) + cost[i][2] + cost[n - i - 1][0];
+ long nextdp5 = Math.min(Math.min(dp1, dp2), dp3) + cost[i][2] + cost[n - i - 1][1];
+ dp0 = nextdp0;
+ dp1 = nextdp1;
+ dp2 = nextdp2;
+ dp3 = nextdp3;
+ dp4 = nextdp4;
+ dp5 = nextdp5;
+ }
+ long ans = Long.MAX_VALUE;
+ for (long x : new long[] {dp0, dp1, dp2, dp3, dp4, dp5}) {
+ ans = Math.min(ans, x);
+ }
+ return ans;
+ }
+}
diff --git a/src/main/java/g3401_3500/s3429_paint_house_iv/readme.md b/src/main/java/g3401_3500/s3429_paint_house_iv/readme.md
new file mode 100644
index 000000000..8610512fd
--- /dev/null
+++ b/src/main/java/g3401_3500/s3429_paint_house_iv/readme.md
@@ -0,0 +1,53 @@
+3429\. Paint House IV
+
+Medium
+
+You are given an **even** integer `n` representing the number of houses arranged in a straight line, and a 2D array `cost` of size `n x 3`, where `cost[i][j]` represents the cost of painting house `i` with color `j + 1`.
+
+The houses will look **beautiful** if they satisfy the following conditions:
+
+* No **two** adjacent houses are painted the same color.
+* Houses **equidistant** from the ends of the row are **not** painted the same color. For example, if `n = 6`, houses at positions `(0, 5)`, `(1, 4)`, and `(2, 3)` are considered equidistant.
+
+Return the **minimum** cost to paint the houses such that they look **beautiful**.
+
+**Example 1:**
+
+**Input:** n = 4, cost = [[3,5,7],[6,2,9],[4,8,1],[7,3,5]]
+
+**Output:** 9
+
+**Explanation:**
+
+The optimal painting sequence is `[1, 2, 3, 2]` with corresponding costs `[3, 2, 1, 3]`. This satisfies the following conditions:
+
+* No adjacent houses have the same color.
+* Houses at positions 0 and 3 (equidistant from the ends) are not painted the same color `(1 != 2)`.
+* Houses at positions 1 and 2 (equidistant from the ends) are not painted the same color `(2 != 3)`.
+
+The minimum cost to paint the houses so that they look beautiful is `3 + 2 + 1 + 3 = 9`.
+
+**Example 2:**
+
+**Input:** n = 6, cost = [[2,4,6],[5,3,8],[7,1,9],[4,6,2],[3,5,7],[8,2,4]]
+
+**Output:** 18
+
+**Explanation:**
+
+The optimal painting sequence is `[1, 3, 2, 3, 1, 2]` with corresponding costs `[2, 8, 1, 2, 3, 2]`. This satisfies the following conditions:
+
+* No adjacent houses have the same color.
+* Houses at positions 0 and 5 (equidistant from the ends) are not painted the same color `(1 != 2)`.
+* Houses at positions 1 and 4 (equidistant from the ends) are not painted the same color `(3 != 1)`.
+* Houses at positions 2 and 3 (equidistant from the ends) are not painted the same color `(2 != 3)`.
+
+The minimum cost to paint the houses so that they look beautiful is `2 + 8 + 1 + 2 + 3 + 2 = 18`.
+
+**Constraints:**
+
+* 2 <= n <= 105
+* `n` is even.
+* `cost.length == n`
+* `cost[i].length == 3`
+* 0 <= cost[i]\[j] <= 105
\ No newline at end of file
diff --git a/src/main/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/Solution.java b/src/main/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/Solution.java
new file mode 100644
index 000000000..0b343f7c6
--- /dev/null
+++ b/src/main/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/Solution.java
@@ -0,0 +1,45 @@
+package g3401_3500.s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays;
+
+// #Hard #Array #Math #Stack #Monotonic_Stack #2025_01_22_Time_27_(99.40%)_Space_56.05_(94.64%)
+
+public class Solution {
+ public long minMaxSubarraySum(int[] nums, int k) {
+ long sum = solve(nums, k);
+ for (int i = 0; i < nums.length; i++) {
+ nums[i] = -nums[i];
+ }
+ return sum - solve(nums, k);
+ }
+
+ private long solve(int[] nums, int k) {
+ int n = nums.length;
+ int[] left = new int[n];
+ int[] right = new int[n];
+ int[] st = new int[n];
+ int top = -1;
+ for (int i = 0; i < n; i++) {
+ int num = nums[i];
+ while (top != -1 && num < nums[st[top]]) {
+ right[st[top--]] = i;
+ }
+ left[i] = top == -1 ? -1 : st[top];
+ st[++top] = i;
+ }
+ while (0 <= top) {
+ right[st[top--]] = n;
+ }
+ long ans = 0;
+ for (int i = 0; i < n; i++) {
+ int num = nums[i];
+ int l = Math.min(i - left[i], k);
+ int r = Math.min(right[i] - i, k);
+ if (l + r - 1 <= k) {
+ ans += (long) num * l * r;
+ } else {
+ long cnt = (long) (k - r + 1) * r + (long) (l + r - k - 1) * (r + k - l) / 2;
+ ans += num * cnt;
+ }
+ }
+ return ans;
+ }
+}
diff --git a/src/main/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/readme.md b/src/main/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/readme.md
new file mode 100644
index 000000000..a728efe17
--- /dev/null
+++ b/src/main/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/readme.md
@@ -0,0 +1,53 @@
+3430\. Maximum and Minimum Sums of at Most Size K Subarrays
+
+Hard
+
+You are given an integer array `nums` and a **positive** integer `k`. Return the sum of the **maximum** and **minimum** elements of all **non-empty subarrays** with **at most** `k` elements.
+
+**Example 1:**
+
+**Input:** nums = [1,2,3], k = 2
+
+**Output:** 20
+
+**Explanation:**
+
+The subarrays of `nums` with at most 2 elements are:
+
+| **Subarray** | Minimum | Maximum | Sum |
+|--------------|---------|---------|-----|
+| `[1]` | 1 | 1 | 2 |
+| `[2]` | 2 | 2 | 4 |
+| `[3]` | 3 | 3 | 6 |
+| `[1, 2]` | 1 | 2 | 3 |
+| `[2, 3]` | 2 | 3 | 5 |
+| **Final Total** | | | 20 |
+
+The output would be 20.
+
+**Example 2:**
+
+**Input:** nums = [1,-3,1], k = 2
+
+**Output:** \-6
+
+**Explanation:**
+
+The subarrays of `nums` with at most 2 elements are:
+
+| **Subarray** | Minimum | Maximum | Sum |
+|----------------|---------|---------|------|
+| `[1]` | 1 | 1 | 2 |
+| `[-3]` | -3 | -3 | -6 |
+| `[1]` | 1 | 1 | 2 |
+| `[1, -3]` | -3 | 1 | -2 |
+| `[-3, 1]` | -3 | 1 | -2 |
+| **Final Total**| | | -6 |
+
+The output would be -6.
+
+**Constraints:**
+
+* `1 <= nums.length <= 80000`
+* `1 <= k <= nums.length`
+* -106 <= nums[i] <= 106
\ No newline at end of file
diff --git a/src/test/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/SolutionTest.java b/src/test/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/SolutionTest.java
new file mode 100644
index 000000000..2ee238636
--- /dev/null
+++ b/src/test/java/g3401_3500/s3423_maximum_difference_between_adjacent_elements_in_a_circular_array/SolutionTest.java
@@ -0,0 +1,18 @@
+package g3401_3500.s3423_maximum_difference_between_adjacent_elements_in_a_circular_array;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void maxAdjacentDistance() {
+ assertThat(new Solution().maxAdjacentDistance(new int[] {1, 2, 4}), equalTo(3));
+ }
+
+ @Test
+ void maxAdjacentDistance2() {
+ assertThat(new Solution().maxAdjacentDistance(new int[] {-5, -10, -5}), equalTo(5));
+ }
+}
diff --git a/src/test/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/SolutionTest.java b/src/test/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/SolutionTest.java
new file mode 100644
index 000000000..db9f6ac08
--- /dev/null
+++ b/src/test/java/g3401_3500/s3424_minimum_cost_to_make_arrays_identical/SolutionTest.java
@@ -0,0 +1,20 @@
+package g3401_3500.s3424_minimum_cost_to_make_arrays_identical;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void minCost() {
+ assertThat(
+ new Solution().minCost(new int[] {-7, 9, 5}, new int[] {7, -2, -5}, 2),
+ equalTo(13L));
+ }
+
+ @Test
+ void minCost2() {
+ assertThat(new Solution().minCost(new int[] {2, 1}, new int[] {2, 1}, 0), equalTo(0L));
+ }
+}
diff --git a/src/test/java/g3401_3500/s3425_longest_special_path/SolutionTest.java b/src/test/java/g3401_3500/s3425_longest_special_path/SolutionTest.java
new file mode 100644
index 000000000..f848f5887
--- /dev/null
+++ b/src/test/java/g3401_3500/s3425_longest_special_path/SolutionTest.java
@@ -0,0 +1,25 @@
+package g3401_3500.s3425_longest_special_path;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void longestSpecialPath() {
+ assertThat(
+ new Solution()
+ .longestSpecialPath(
+ new int[][] {{0, 1, 2}, {1, 2, 3}, {1, 3, 5}, {1, 4, 4}, {2, 5, 6}},
+ new int[] {2, 1, 2, 1, 3, 1}),
+ equalTo(new int[] {6, 2}));
+ }
+
+ @Test
+ void longestSpecialPath2() {
+ assertThat(
+ new Solution().longestSpecialPath(new int[][] {{1, 0, 8}}, new int[] {2, 2}),
+ equalTo(new int[] {0, 1}));
+ }
+}
diff --git a/src/test/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/SolutionTest.java b/src/test/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/SolutionTest.java
new file mode 100644
index 000000000..b4fb1df5d
--- /dev/null
+++ b/src/test/java/g3401_3500/s3426_manhattan_distances_of_all_arrangements_of_pieces/SolutionTest.java
@@ -0,0 +1,18 @@
+package g3401_3500.s3426_manhattan_distances_of_all_arrangements_of_pieces;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void distanceSum() {
+ assertThat(new Solution().distanceSum(2, 2, 2), equalTo(8));
+ }
+
+ @Test
+ void distanceSum2() {
+ assertThat(new Solution().distanceSum(1, 4, 3), equalTo(20));
+ }
+}
diff --git a/src/test/java/g3401_3500/s3427_sum_of_variable_length_subarrays/SolutionTest.java b/src/test/java/g3401_3500/s3427_sum_of_variable_length_subarrays/SolutionTest.java
new file mode 100644
index 000000000..3f910b5f6
--- /dev/null
+++ b/src/test/java/g3401_3500/s3427_sum_of_variable_length_subarrays/SolutionTest.java
@@ -0,0 +1,18 @@
+package g3401_3500.s3427_sum_of_variable_length_subarrays;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void subarraySum() {
+ assertThat(new Solution().subarraySum(new int[] {2, 3, 1}), equalTo(11));
+ }
+
+ @Test
+ void subarraySum2() {
+ assertThat(new Solution().subarraySum(new int[] {3, 1, 1, 2}), equalTo(13));
+ }
+}
diff --git a/src/test/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/SolutionTest.java b/src/test/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/SolutionTest.java
new file mode 100644
index 000000000..24e7225e8
--- /dev/null
+++ b/src/test/java/g3401_3500/s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences/SolutionTest.java
@@ -0,0 +1,18 @@
+package g3401_3500.s3428_maximum_and_minimum_sums_of_at_most_size_k_subsequences;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void minMaxSums() {
+ assertThat(new Solution().minMaxSums(new int[] {1, 2, 3}, 2), equalTo(24));
+ }
+
+ @Test
+ void minMaxSums2() {
+ assertThat(new Solution().minMaxSums(new int[] {5, 0, 6}, 1), equalTo(22));
+ }
+}
diff --git a/src/test/java/g3401_3500/s3429_paint_house_iv/SolutionTest.java b/src/test/java/g3401_3500/s3429_paint_house_iv/SolutionTest.java
new file mode 100644
index 000000000..4f718128b
--- /dev/null
+++ b/src/test/java/g3401_3500/s3429_paint_house_iv/SolutionTest.java
@@ -0,0 +1,27 @@
+package g3401_3500.s3429_paint_house_iv;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void minCost() {
+ assertThat(
+ new Solution().minCost(4, new int[][] {{3, 5, 7}, {6, 2, 9}, {4, 8, 1}, {7, 3, 5}}),
+ equalTo(9L));
+ }
+
+ @Test
+ void minCost2() {
+ assertThat(
+ new Solution()
+ .minCost(
+ 6,
+ new int[][] {
+ {2, 4, 6}, {5, 3, 8}, {7, 1, 9}, {4, 6, 2}, {3, 5, 7}, {8, 2, 4}
+ }),
+ equalTo(18L));
+ }
+}
diff --git a/src/test/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/SolutionTest.java b/src/test/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/SolutionTest.java
new file mode 100644
index 000000000..0e29fbc5b
--- /dev/null
+++ b/src/test/java/g3401_3500/s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays/SolutionTest.java
@@ -0,0 +1,18 @@
+package g3401_3500.s3430_maximum_and_minimum_sums_of_at_most_size_k_subarrays;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void minMaxSubarraySum() {
+ assertThat(new Solution().minMaxSubarraySum(new int[] {1, 2, 3}, 2), equalTo(20L));
+ }
+
+ @Test
+ void minMaxSubarraySum2() {
+ assertThat(new Solution().minMaxSubarraySum(new int[] {1, -3, 1}, 2), equalTo(-6L));
+ }
+}