3625. Count Number of Trapezoids II #2490
-
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to count trapezoids (quadrilaterals with at least one pair of parallel sides) from given points. Approach:
Let's implement this solution in PHP: 3625. Count Number of Trapezoids II <?php
/**
* @param Integer[][] $points
* @return Integer
*/
function countTrapezoids($points) {
$n = count($points);
if ($n < 4) return 0;
// slope → (lineSignature → count)
$cnt1 = [];
// midpointSignature → (slopeSignature → count)
$cnt2 = [];
for ($i = 0; $i < $n; $i++) {
[$x1, $y1] = $points[$i];
for ($j = 0; $j < $i; $j++) {
[$x2, $y2] = $points[$j];
$dx = $x2 - $x1;
$dy = $y2 - $y1;
// ---- Normalize slope (dy, dx) ----
if ($dx == 0) {
$slope = "V,1"; // vertical
} else {
$g = gcd(abs($dx), abs($dy));
$dy2 = intdiv($dy, $g);
$dx2 = intdiv($dx, $g);
// Fix sign: dx must be positive for uniqueness
if ($dx2 < 0) {
$dx2 = -$dx2;
$dy2 = -$dy2;
}
$slope = $dy2 . "," . $dx2;
}
// ---- Normalize line (A,B,C): Ax+By+C=0 ----
// For slope (dy,dx): line perpendicular has A = dy, B = -dx
if ($dx == 0) {
// vertical x = x1 → 1*x + 0*y - x1 = 0
$A = 1; $B = 0; $C = -$x1;
} else {
// slope dy/dx → line eq: dy*x - dx*y + C = 0
$A = $dy;
$B = -$dx;
// solve for C: A*x + B*y + C = 0 → C = -(Ax + By)
$C = -($A * $x1 + $B * $y1);
}
$g = gcd(gcd(abs($A), abs($B)), abs($C));
if ($g != 0) {
$A = intdiv($A, $g);
$B = intdiv($B, $g);
$C = intdiv($C, $g);
}
// Fix sign for uniqueness
if ($A < 0 || ($A == 0 && $B < 0)) {
$A = -$A; $B = -$B; $C = -$C;
}
$lineKey = "$A,$B,$C";
// ---- Update cnt1: slope → lines ----
if (!isset($cnt1[$slope][$lineKey])) {
$cnt1[$slope][$lineKey] = 0;
}
$cnt1[$slope][$lineKey]++;
// ---- Update cnt2: midpoint+ slope = parallelogram detection ----
$mx = $x1 + $x2; // midpoint numerator only is enough
$my = $y1 + $y2;
$midKey = "$mx,$my";
if (!isset($cnt2[$midKey][$slope])) {
$cnt2[$midKey][$slope] = 0;
}
$cnt2[$midKey][$slope]++;
}
}
$ans = 0;
// ---- Count trapezoids: sum over slope-buckets ----
foreach ($cnt1 as $slope => $lineMap) {
$sum = 0;
foreach ($lineMap as $cnt) {
$ans += $sum * $cnt;
$sum += $cnt;
}
}
// ---- Subtract parallelograms: they were counted twice ----
foreach ($cnt2 as $midKey => $slopes) {
$sum = 0;
foreach ($slopes as $cnt) {
$ans -= $sum * $cnt;
$sum += $cnt;
}
}
return $ans;
}
// gcd
function gcd(int $a, int $b): int
{
while ($b != 0) {
[$a, $b] = [$b, $a % $b];
}
return $a;
}
// Test cases
echo countTrapezoids([[-3,2],[3,0],[2,3],[3,2],[2,-3]]) . "\n"; // Output: 2
echo countTrapezoids([[0,0],[1,0],[0,1],[2,1]]) . "\n"; // Output: 1
echo countTrapezoids([[82,7],[82,-9],[82,-52],[82,78]]) . "\n"; // Output: 0
echo countTrapezoids([[83,-25],[74,11],[-65,-25],[33,-25],[17,-25],[1,30],[-84,-25],[1,-25],[1,-92],[-87,13]]) . "\n"; // Output: 0
?>Explanation:
|
Beta Was this translation helpful? Give feedback.
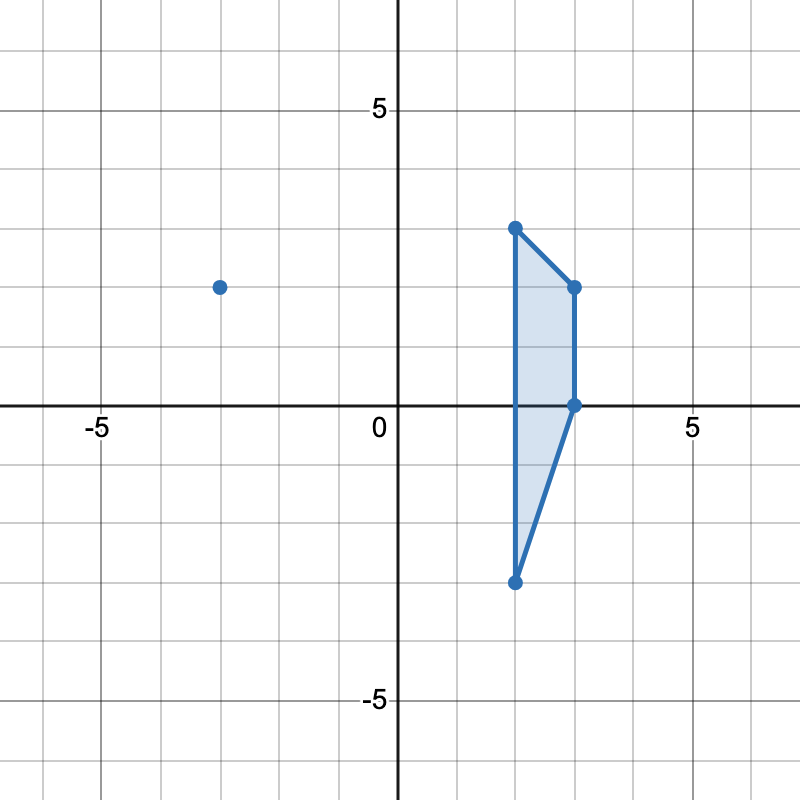
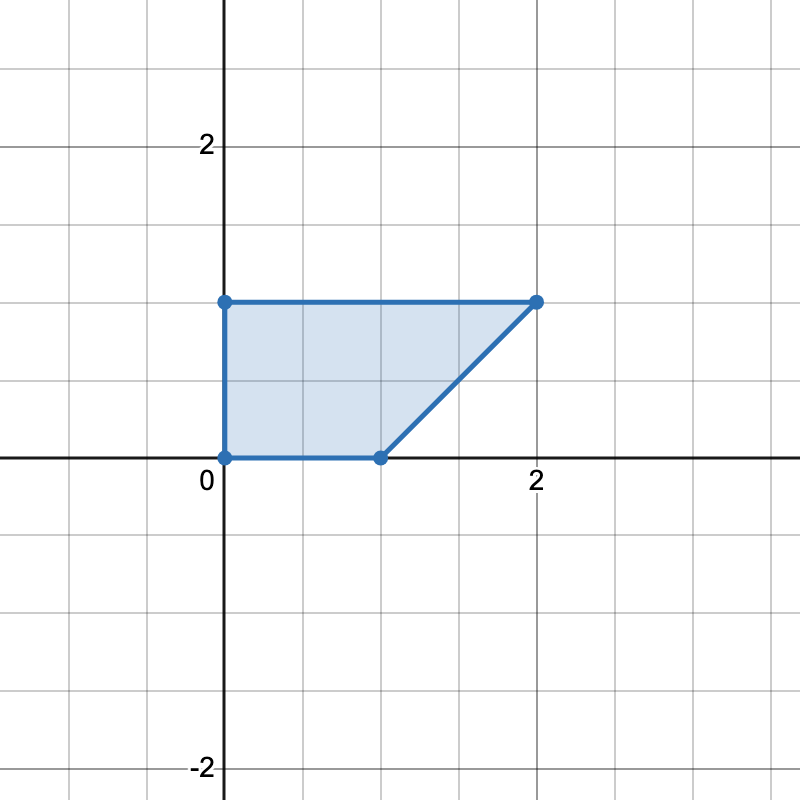
We need to count trapezoids (quadrilaterals with at least one pair of parallel sides) from given points.
Approach:
Precompute all point pairs (i, j) → each pair defines a segment.
For each pair:
(dy, dx); vertical lines treated separately.(A, B, C)as the signature of that infinite line.(x₁ + x₂, y₁ + y₂)without division (for parallelogram detection).Maintain:
cnt1[slope][lineSignature]→ counts how many segments lie on the same infinite line with same slope
→ used to count pairs of parallel but non-collinear segments (candidate trapezoid bases).
cnt2[midpointSignature][slope]→ c…