-
Notifications
You must be signed in to change notification settings - Fork 0
SQLGraphExplorer‐10
-
我先读完了《Translating View Updates Using Inversion of Relational Algebra》的后半部分。但是一开始读完有点晕。
-
该论文结尾处提到了此问题的相关论文,于是我又去读了《Efficiently Updating Materialized Views》。
- 该论文在 Introduntion 部分提及了传统的视图更新问题(逆向问题):将 对数据库视图的修改 翻译为 对底层数据库的修改 。
- 但令人心寒的是,这篇解决的问题是正向的效率问题:当修改底层数据库时,我们更新数据库视图的传统方式是重新跑一遍关系表达式,但这效率很低,于是该论文目标是寻找一种有效率的算法来让数据库视图与底层数据库保持同步。(莫名联想到修改源代码时加快重新编译的速度)
- 总而言之,这篇论文方向歪了,于是我读完 Introduntion 就放弃了。并以“view update problem”为关键字去找了半天。
-
找到了关于“view update problem”的一篇论文——《Relational lenses: a language for updatable views》。读这篇文章有两个目标:
- 基础目标:了解这个问题的背景,辅助理解论文 1
-
没实现的目标:看懂解决视图更新问题的另一种方法,但是读到一半就全晕了。。。
- 一个 transaction 是一系列更新(update)的有限序列
$T=u_1,...,u_m$ -
$u_i$ 是一个更新(update),该更新将一个元组集合(tuple set)插入$R_i$,或者从$R_i$中删除一个元组集合 - 将一个元组集合$\tau$插入$R$可形式化表示为:$ins(\tau,R)$
- 将一个元组集合$\tau$从$R$中删除可形式化表示为:$del(\tau,R)$
$T$ 是一个 tranaction,$\tau$是一个元组集合,$\mathcal{R}$是 relation schema,$r$是关系$R$的一个实例
- 如果$u=ins(\tau,R)$是在关系 R 上的一个更新,那么$ins(\tau,r)$的效果是:$r:=r\cup\tau$。即将$\tau$插入到关系$r$中。
- 如果$u=del(\tau,R)$是在关系 R 上的一个更新,那么$del(\tau,r)$的效果是:$r:=r-\tau$。即将$\tau$从关系$r$中删除。
-
$T'=u_1',u_2',...,u_k'$ 是$T=u_1,u_2,...,u_k$的子-transaction,如果满足以下条件:$u_i=upd(\tau_i,R_i),u_i'=upd(\tau_i',R_i')$ $R_i'=R_i,\tau_i'\subseteq\tau_i$
-
$T_R$ :读作$T$的 R-transaction,实际上就是对$T$的一系列更新进行过滤(只挑出关系 R 上的更新)-
$T_R$ 是$T$的子-transaction -
$T_R$ 包含了$T$中所有在$R$之上的更新(update) $\forall R_i\neq R,u_i=upd(\tau_i,R_i)表示\tau_i=\emptyset$
-
-
$eff(T_R,r)$ :表示$T_R$作用于$r$上所产生的效果,代表在$r$上应用$T_R$之后关系$r$的新状态。 - 如果一个 transaction 只包含插入(或删除)更新,那么该 transaction 可被称作插入-transaction(或删除-transaction)
-
$u_i=upd(\tau_i,R_i)$ ,$upd=ins/del$- 这表明作用在关系$r_1\cup\tau_1,...,r_n\cup\tau_n$(或$r_1-\tau_1,...,r_n-\tau_n$)之上的表达式 E 会生成元组 t
-
两个形式化定义:
- 如果$\mathcal{U}(t,E)$是插入,那么$t\in \mathcal{E}(eff(T_{R_1},r_1),...,eff(T_{R_n},r_n))$
- 如果$\mathcal{U}(t,E)$是删除,那么$t\notin \mathcal{E}(eff(T_{R_1},r_1),...,eff(T_{R_n},r_n))$
-
这表明每个试图更新的转化都是一个实现该更新的“最小”-transaction
-
对于$T$的每个子-transaction
$T’$ ,上面的第 1 点不成立
表达式 E 不含 difference 操作符,$\mathcal{U}(t,E)$的每个转化可以写作:$T=upd((\tau_1,R_1),...,(\tau_n,R_n))$
-
Relation:
- employee relation —— emp : <Ename, Pname>
- department relation —— dept : <Ename, Dname>
-
View : v
-
insert view udpate :
$\mathcal{U}(<Mary,CS>,E)$ , 作用于视图 v 上 -
Transaction :
$T=ins(({<Mary,P>},emp),({<Mary,CS>},dept))$
给定一个数据库的视图更新$\mathcal{U}$,找到$\mathcal{U}$的所有转换(translation)的集合。解决方法基于逆像(inverse image)
-
Relation:
-
employee relation —— emp : <Ename, Pname>
-
Ename Pname John P
-
-
department relation —— dept : <Ename, Dname>
-
Ename Dname John M
-
-
-
View : v,是如下表达式 E 的视图
-
$E=\Pi_{Ename,Dname}(\sigma_{Pname=P}(Emp\bowtie Dept))$ -
Ename Dname John M
-
-
-
delete view update :
$Del(<John,M>,E)$ -
$Del(<John,M>,E)$ 的两个转换为:$T=del((<John,P>,Emp),(\emptyset,Dept))$ $T'=del((\emptyset,Emp),(<John,M>,Dept))$ -
$T''=del((<John,P>,Emp),(<John,M>,Dept))$ ,由于$T''$不是 minimal change,故不考虑。
$Inv(<John,M>,E)={(<John,P>,<John,M>)}$
-
- 对于$T$:$Inv_1={(<John,P>,<John,M>)}$,${Inv_1}$是$Inv$的一个划分
- 对于$T'$:$Inv_2={(<John,P>,<John,M>)}$,${Inv_2}$是$Inv$的一个划分
- 给定一个关系表达式
$E(R_1,...,R_n)$ - 一个定义在 sch(E)上的元组 t
- 一个视图更新$\mathcal{U}(t,E)$
- 那么$\mathcal{U}(t,E)$的一个转化(translation)可以按以下方式,从集合$Inv(t,E)$中构建:
-
$\mathcal{U}(t,E)$ 是插入视图更新:根据 Proposition 5.1,$Inv(t,E)$中的每个计算结果,对应于$\mathcal{U}(t,E)$的每个 translation。 -
$\mathcal{U}(t,E)$ 是删除视图更新:根据 Proposition 5.1,$Inv(t,E)$的每个划分(形式化写做${Inv_1,...,Inv_n}$),对应于$\mathcal{U}(t,E)$的每个 translation(形式化写做$del((\tau_1,R_1),...,(\tau_n,R_n))$)。
集合$\tau_i$可以按照下面的规则,从集合$Inv(t,E)$中构建出来:
版本一(new version):
$Inv_{i-1}:={N\in Inv(t,E)\ |\ N_{i-1}\in\tau_{i-1}}$ $Inv(t,E):=Inv(t,E)-Inv_{i-1}$ $\tau_i={N_i\ |\ N\in Inv(t,E),N_i\neq \epsilon }$
版本二(old version):
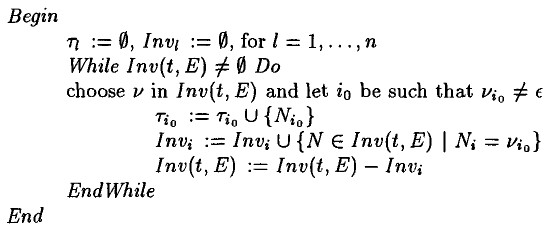
-
Relation:
-
R1 : <A,B>
-
A B a b a b’
-
-
R2 : <B,C>
-
B C b c b’ c
-
-
R3 : <A,C>
-
A C a’ c’
-
-
-
Expression :
$E=\Pi_{AC}(\sigma_{B\ge b}(R_1\bowtie R_2))\cup R_3$ -
A C a c a’ c’
-
-
$dom_B={b,b'}$ -
Inverse :
$Inv(ac,E)={(ab,bc,\epsilon),(ab',b'c,\epsilon),(\epsilon,\epsilon,ac)}$
我们按照以下方式,选择$Del(ac,E)$的两个转化(
$del((\tau_1,R_1),...,(\tau_n,R_n))$ )
-
选择
$(ab',b'c,\epsilon)$ 中的第二个元组$b'c$,并将其放入$\tau_2$。即$b'c\in\tau_2$-
$\tau_2={b'c}$ ,$Inv_2={(ab',b'c,\epsilon)}$ $Inv(t,E)={(ab,bc,\epsilon),(\epsilon,\epsilon,ac)}$
-
$\tau_3={ac}$ ,$Inv_3={(\epsilon,\epsilon,ac)}$ $Inv(t,E)={(ab,bc,\epsilon)}$
-
$\tau_1={ab}$ ,$Inv_1={(ab,bc,\epsilon)}$ $Inv(t,E)=\emptyset$
$T=del(({ab},r_1),({b'c},r_2),({ac},r3))$
-
-
选择
$(ab,bc,\epsilon)$ 中的第一个元组$ab$,并将其放入$\tau_1$。即$ab\in\tau_1$-
$\tau_1={ab}$ ,$Inv_1={(ab,bc,\epsilon)}$ $Inv(t,E)={(ab',b'c,\epsilon),(\epsilon,\epsilon,ac)}$
-
$\tau_1={ab,ab'}$ ,$Inv_1={(ab,bc,\epsilon),(ab',b'c,\epsilon)}$ $Inv(t,E)={(\epsilon,\epsilon,ac)}$
-
$\tau_3={ac}$ ,$Inv_3={(\epsilon,\epsilon,ac)}$ $Inv(t,E)=\emptyset$
$T=del(({ab,ab'},r_1),(\emptyset,r_2),({ac},r_3))$
-
- 强确定性更新:与数据库状态无关的确定性更新
- 弱确定性更新:与数据库状态有关的确定性更新
一个视图更新
$\mathcal{U}(t,E)$ 是强确定性的,如果它有一个单独的转化。但有一些例外情况如下:
- 如果$E=R\cup R$,那么$Ins(t,E)$有两个转化:$T_1=ins((\epsilon,t),(t,\epsilon));T_1=ins((t,\epsilon),(\epsilon,t))$
- 如果$E=R\cap R$,那么$Del(t,E)$有两个转化:$T_1=del((\epsilon,t),(t,\epsilon));T_1=del((t,\epsilon),(\epsilon,t))$
限制条件:
- 关系表达式是正向的
- 关系表达式不包含同一关系符号的多次出现
如果对于所有的$i\neq j,R_i\neq R_j$,那么$Ins(t,E)$是强确定性的 当且仅当
如果$t_i\in N,t_i\neq\epsilon,N\in Inv(t,E)$,那么存在属于$Del(t,E)$的一个转化$T=del((\tau_1,r_1),...,(\tau_n,r_n))$,使得$t_i\in\tau_i$
如果对于所有的$i\neq j,R_i\neq R_j$,那么$Del(t,E)$是强确定性的 当且仅当
在给定数据库上的变化数量:具体地说就是,当针对数据库的当前实例处理给定视图更新的转换时,实际上被插入或删除的元组数量。
-
upd=ins:
$\phi(T)=|\tau_1-r_1|+...+|\tau_n-r_n|$ -
upd=del:
$\phi(T)=|\tau_1\cap r_1|+...+|\tau_n\cap r_n|$
如果$\mathcal{T}$是$\mathcal{U}(t,E)$的所有转化的集合,$I=(r_1,...,r_n)$,那么我们可以定义最小变化如下:
if
-
relational expression:
$E=\Pi_{AC}(\sigma_{B\geq b}(R_1\bowtie R_2))$ $Inv(ac,E)={(ab,bc),(ab',b'c)},dom_B={b',b}$
假设$r_1={ab},r_2={\emptyset}$
-
$Ins(ac,E)$ 的两个转化为:$T_1=ins((ab,R_1),(bc,R_2))\Longrightarrow\phi(T_1)=|{ab}-r_1|+|{bc}-r_2|=1$ $T_2=ins((ab',R_1),(b'c,R_2))\Longrightarrow\phi(T_2)=|{ab'}-r_1|+|{b'c}-r_2|=2$ $\phi(T1)<\phi(T_2)\Longrightarrow T_1是关系实例I=(r_1,r_2)上的保障最小变化的转化$
-
$Del(ac,E)$ 的四个转化为:$T_1=del(({ab,ab'},R_1),(\emptyset,R_2))\Longrightarrow\phi(T_1)=|{ab,ab'}\cap r_1|+|\emptyset \cap r_2|=1$ $T_2=del(({ab},R_1),({b'c},R_2))\Longrightarrow\phi(T_2)=|{ab}\cap r_1|+|{b'c} \cap r_2|=1$ $T_3=del(({ab'},R_1),({bc},R_2))\Longrightarrow\phi(T_3)=|{ab'}\cap r_1|+|{bc} \cap r_2|=0$ $T_4=del((\emptyset,R_1),({bc,b'c},R_2))\Longrightarrow\phi(T_4)=|\emptyset\cap r_1|+|{bc,b'c} \cap r_2|=0$ -
$T_3和T_4$ 是关系实例$I=(r_1,r_2)$上的保障最小变化的转化
-
强确定性的视图更新:
-
$\mathcal{U}(t,E)=Ins(t,E)$ : 如果$|Inv(t,E)|=1$,不妨设$Inv(t,E)={(t_1,...,t_n)}$,则我们可以执行如下的数据库更新:$ins((t_1,R_1),...,(t_n,R_n))$ -
$\mathcal{U}(t,E)=Del(t,E)$ : 如果$Inv(t,E)$中的每个 k-元组都是一元(unary)的,那么我们可以使用 从 Inverse 中计算 Translation 中提及的算法来计算转化,最后我们可以执行如下的数据库更新:$del((\tau_1,R_1),...,(\tau_n,R_n))$
-
补充:一个k-元组是一元的,如果其满足以下形式:
$(t)$ $(\epsilon,...,\epsilon,t,\epsilon,...,\epsilon)$
-
弱确定性的视图更新:
- 如果存在一个独一无二的视图更新转化
$T$ ,$T$ 可保证数据库实例$(r_1,...,r_n)$的最小变化,那么我们可以再数据库上执行$T$
- 如果存在一个独一无二的视图更新转化
-
如果 1 和 2 的条件都不满足,则使用 [BL97](没找到) 中提及的方法。还有另外两篇相关论文介绍了视图维护的问题。
Efficiently Updating Materialized Views(读完 Introduction 发现方向歪了,遂放弃)
在一个关系数据库系统中,一个数据库由 基础关系 和 派生关系 组成:
- 基础关系:可以看作源关系
- 派生关系:由一个关系表达式(例如一个在基本关系上执行的查询)定义的关系
派生关系可以是:
- 虚拟的(virtual):对应于传统概念中的视图
- 实例化的(materialized):结果关系实际上被存储
当更新基础关系时,实例化视图可能也需要修改。通过重新计算定义实例化视图的关系表达式,就可以始终使实例化视图保持最新。但是完全地重新计算关系表达式的代价是无法接受的。
- 传统的视图更新问题:允许用户直接向视图进行更新,困难点在于:如何将根据 视图表达的更新 转换为 对基础关系的更新 。
- 本文的视图更新问题:用户只可以更新基础关系,对视图的直接更新不予考虑。
因此,本文不是为了找到派生关系上的更新的转化,而是着眼于寻找有效的方法,将实例化视图保持与基本关系同步。
Abstract: 将经常访问的用户视图具体化可以加快查询处理速度。然而,只有充分维护实体化视图,才能避免在响应查询时访问基础关系的需要。我们提出了一种方法,首先对基础关系的所有数据库更新进行过滤,剔除那些不可能影响视图的更新。检测这类更新(称为无关更新)的条件是必要且充分的,并且与数据库状态无关。对于其余的数据库更新,可以采用差分算法来重新评估视图表达式。所提出的算法利用了视图定义表达式和数据库更新操作所提供的知识。