Interpolation support for GeometryPath's

[joris997]

Summary of changes

This pull request introduces the so-called "FunctionBasedPath" and "PointBasedPath". Currently, a muscle is described by a trajectory of points. Whether the trajectory is described by literal path points or by wrapping objects, the evaluation of lengths, lengthening speed, and moment arm can take considerable time (wrapping objects especially!). This PR, for each muscle, samples the affecting coordinates (unlock coordinate, perturb, see the change in muscle length), samples an n-dimensional grid of muscle lengths, and allows for interpolation to compute the length, lengthening speed, and moment arm.
An alias referring GeometryPath to PointBasedPath is set to make this update compatible with current models.

Inner workings

FunctionBasedPath (FBP) and PointBasedPath (PBP)

As mentioned, this PR introduces FBP and PBP. Both are sub-classes of GeometryPath. Currently, only GeometryPath is defined but this PR creates a distinction between a GeometryPath which is defined by a collection of points and one which is defined by sampling of a grid. PointBasedPath is the original GeometryPath implementation which contains all 'point-related' member functions. FunctionBasedPath contains the same methods but consists of an Interpolation object. The following methods are rewritten to be in accordance with the Interpolation object;

• extendFinalizeFromProperties()
• extendFinalizeConnections(Component)
• getLength(const State)
• setLength(const State, double)
• getLengtheningSpeed(const State)
• setLengtheningSpeed(const State, double)
• computeMomentArm(const State, const Coordinate)
• addInEquivalentForces(const State, double, Vector_, Vector)
• calcLengthAfterPathComputation(const State, const Array)
• computeLengtheningSpeed(const State)
• generateDecorations(..)

Other functions should not be callable for the FBP and therefore throw an OpenSim exception (OPENSIM_THROW)

Method details

getLength()

Using the Interpolator interpolation grid, a length is returned by using a 5th order spline. First, the state given as an argument to the FBP gets filtered of only the relevant affecting coordinates which get put in a vector and passed to getInterp(const std::vector).

getLengtheningSpeed()

The lengthening speed can be computed as the summation of the moment-arm times the coordinateSpeedValue (not changed in this PR) overall affecting coordinates.

computeMomentArm()

The moment-arm is the partial derivative of the length w.r.t. a coordinate. Therefore, the moment-arm is computed with the derivative (getInterpDer). Although initially it was thought out that this can be computed using the derivatives of the 5th order splines, this did not work in the current implementation. Instead, a finite difference derivative is computed. This has sufficient accuracy (step-size is 0.0001).

Others

other methods mentioned above are straightforward changes to the PointBasedPath implementation.

Usage

Accompanying this PR, an additional Tool has been developed (FunctionBasedPathConversionTool) which takes, as arguments, the std::string of a path to a PointBasedPath model, and a string indicating the output model name. You can then use tool.run() in order to generate a model in your build directory along with the accompanying text files containing the sampling data. The tool works as follows:

Interpolation Object

The PBP model, the argument, gets loaded and for each PointBasedPath an Interpolation object is made

Finding affecting coordinates

The n-dimensional grid is made up of a sampling grid of the n affecting coordinates. In FunctionBasedPath.cpp, an implementation is introduced where each coordinate is checked if it affects the GeometryPath under consideration (See coordinateAffectsPBP). These coordinates are then later used for the sampling.

Sampling

Using the affecting coordinates, an n-dimensional grid of GeometryPath lengths gets sampled and added to a 'grid' in the Interpolator constructor.

Print interpolation object

When the whole model has been build using FunctionBasedPath's (each containing an Interpolation object), the model get's printed along with a print-to-file for each Interpolation object. Inside the osim-file of the model, a path points towards the location of the Interpolation print file. This contains the affecting coordinates (with ranges, number of points for the range, etc.) and all the interpolated values).

Load FBP model

When the FBP model is to be loaded, the model-builder looks if it can find the specified interpolation text file it printed earlier. If this file exists, it gets read and the Interpolation object that is a member of a specific FBP gets loaded with the data of this file.

Testing

Speed-up

The main goal of this PR is to improve the computation speed of Forward Dynamic simulations. The Rajagopal model seems to be unfeasible for fast sampling with a sufficiently accurate grid on my machine. Instead, I tested the Arm26 and the Hopper model.
We obtain the following results table based on 23 interpolation pointer per affecting coordinate;

Model	GeometryPath type	Average time (sim-time)	Steps Attempted	Steps Taken	Speed-up
Arm 26	PointBasedPath (old)	918 ms (5.0 s)	996	697
	FunctionBasedPath (interp)	432 ms (5.0 s)	993	687	2.125x faster
Hopper	PointBasedPath (old)	72 ms (1.0 s)	189	134
	FunctionBasedPath (interp)	65 ms (1.0 s)	194	138	1.108x faster

Accuracy

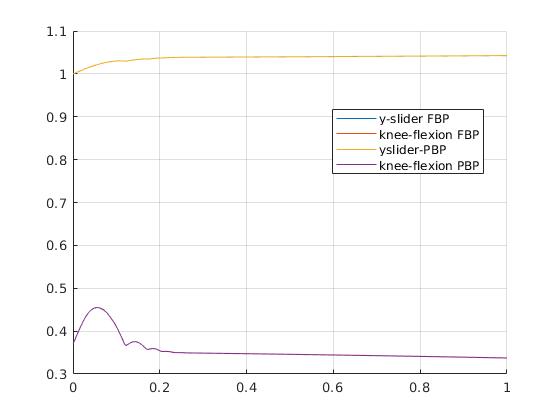
Based on 23 interpolation points per affecting coordinate;

Model	State value	RMS	Max error
Arm26	/r_shoulder_evel/value	0.0048	0.0094
	/r_elbow_flex/value	0.0137	0.0244
Hopper	/yCoord/value	3.0518e-05	7.7702e-05
	/hipFlextion/value	1.2728e-04	5.1314e-0

Which looks a bit like this for the Arm26 model;

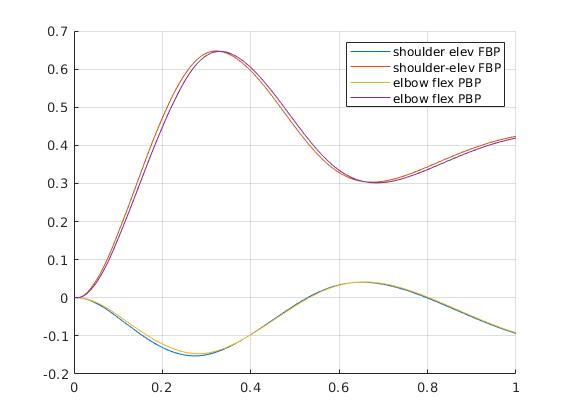
and like this for the Hopper model;

[adamkewley]

This should probably be replaced with OpenSim's command-line parsing conventions. See: https://github.com/opensim-org/opensim-core/blob/master/Applications/opensim-cmd/opensim-cmd_run-tool.h#L70

[adamkewley]

Do we test the accuracy?