pygasflow

pygasflow is a Python package that provides a few handful functions to quickly perform:

• Compressible flow computation in the quasi-1D ideal gasdynamic (perfect gas) regime. The following solvers are implemented:

  • isentropic_solver.
  • fanno_solver.
  • rayleigh_solver.
  • shockwave_solver for normal and oblique shock waves.
  • conical_shockwave_solver.
  • De_Laval_solver and the nozzles sub-module, containing functions and classes to understand convergent-divergent nozzles, Rao's TOP nozzles (Thrust Optmizie Parabolic), Minimum Length nozzle with Method of Characteristics. Nozzles can be used to quickly visualize their geometric differences or to solve the isentropic expansion with the De_Laval_Solver class.

• Aerothermodynamic computations (pygasflow.atd module):

  • Correlations to estimate boundary layer thickness, heat flux and wall shear stress over a flat plate or a stagnation region.
  • Newtonian Flow Theory to estimate the pressure distribution around objects and their aerodynamic characteristics.

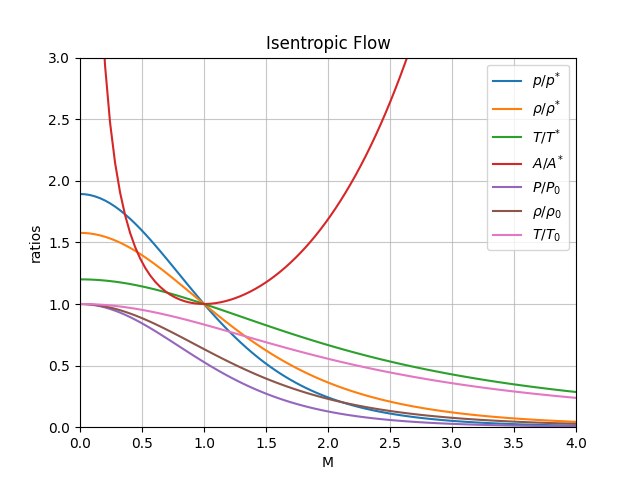
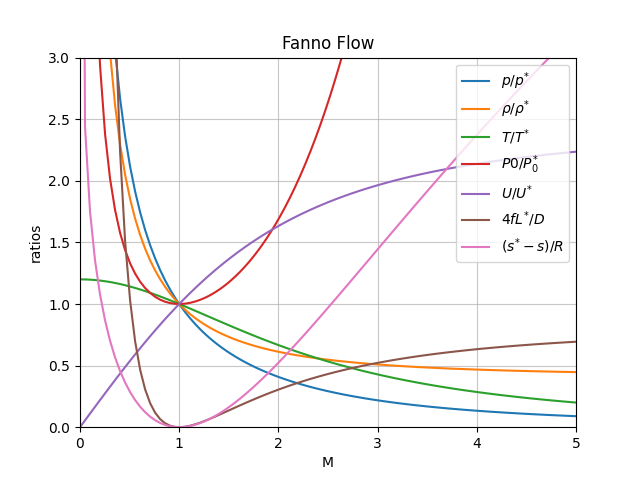
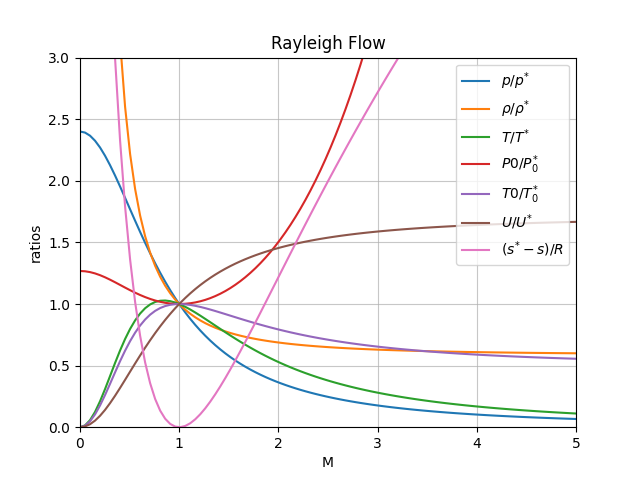
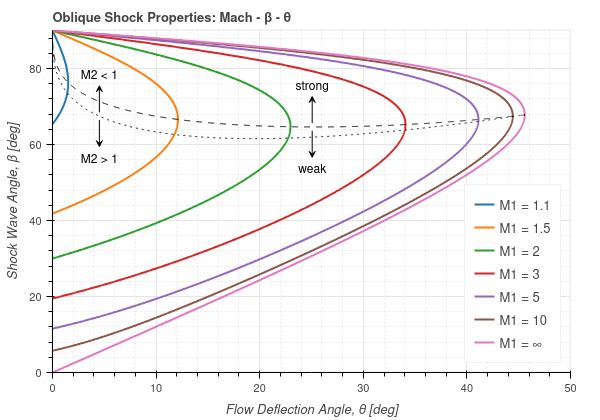
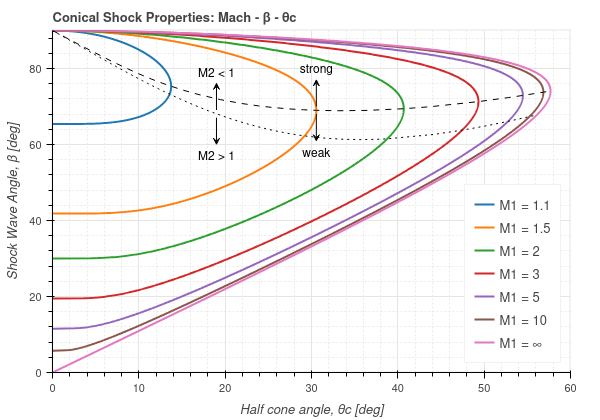
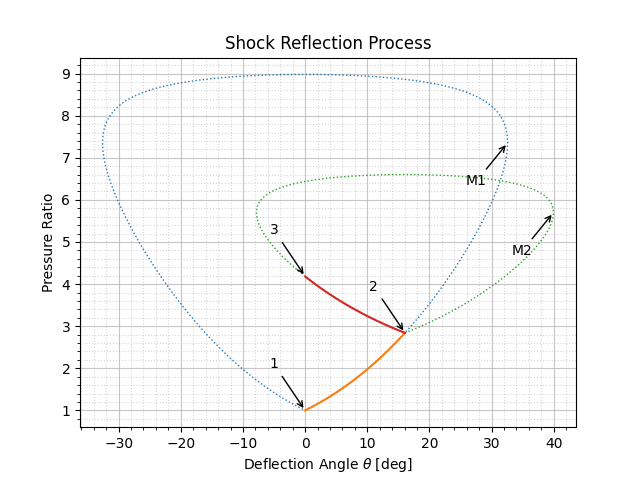
The following charts has been generated with the functions included in this package:

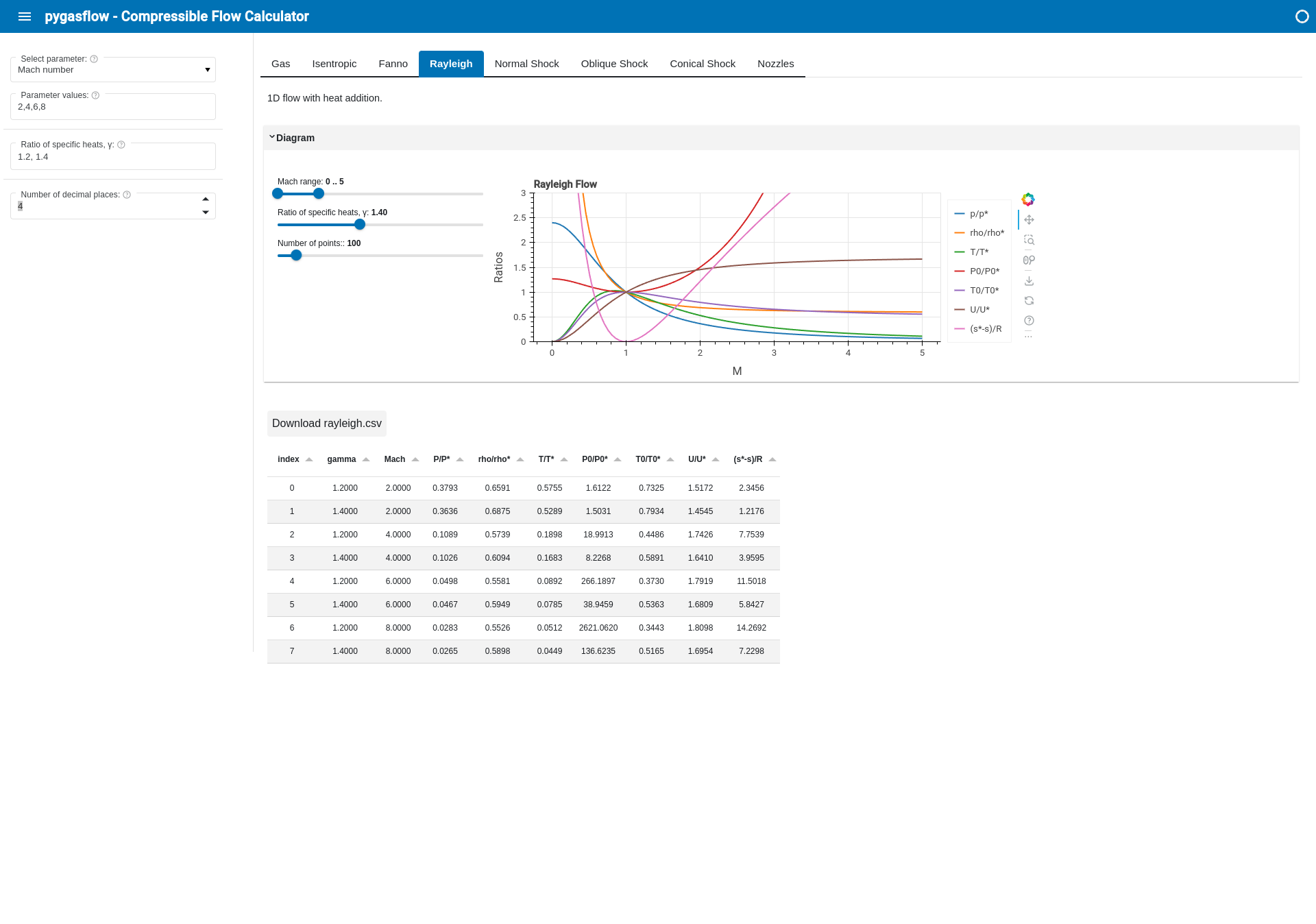
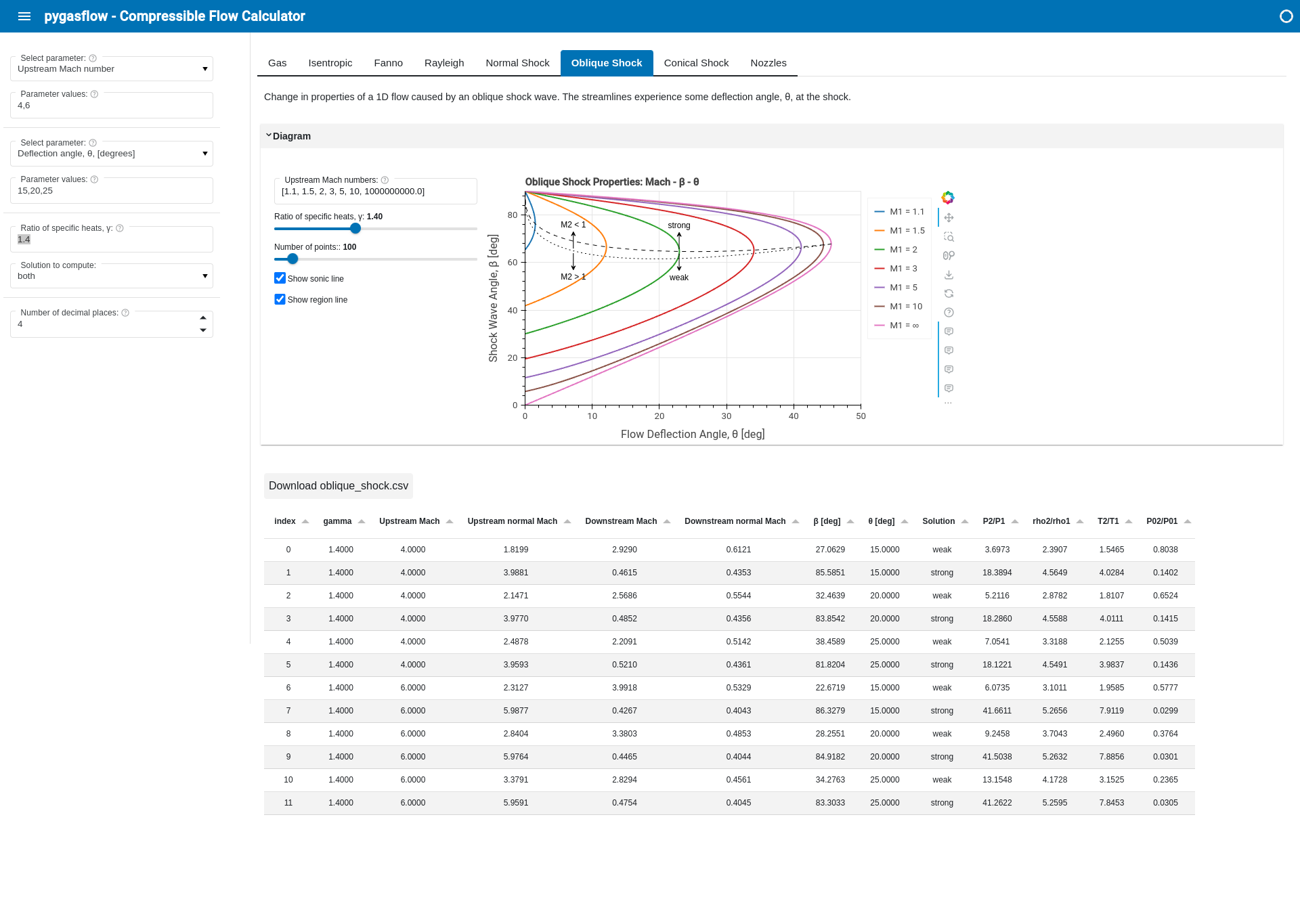
The following screenshots highlights the interactive capabilities implemented in this module:

Development and Support

If you feel like a feature could be implemented, open an issue or create a PR. Implementing new features and fixing bugs requires time and energy too. If you found this module useful and would like to show your appreciation, please consider sponsoring this project with either one of these options:

or

Installation

The repository is avaliable on PyPi:

pip install pygasflow

And also on Conda:

conda install conda-forge::pygasflow

Usage

The easiest way is to call a solver. Let's say you need to solve an isentropic flow:

from pygasflow import isentropic_solver

# optional steps needed to use units with pint
import pint
import pygasflow
ureg = pint.UnitRegistry()
# use short units notation
ureg.formatter.default_format = "~"
# let pygasflow knows which UnitRegistry to use
pygasflow.defaults.pint_ureg = ureg

T1 = 290 * ureg.K
p1 = 1 * ureg.atm

# compute ratios and quantities for an isentropic flow at Mach 2
res = isentropic_solver("m", 2, to_dict=True)
res.show()
# key     quantity
# ----------------------------
# m       M                        2.00000000
# pr      P / P0                   0.12780453
# dr      rho / rho0               0.23004815
# tr      T / T0                   0.55555556
# prs     P / P*                   0.24192491
# drs     rho / rho*               0.36288737
# trs     T / T*                   0.66666667
# urs     U / U*                   1.63299316
# ars     A / A*                   1.68750000
# ma      Mach Angle              30.00000000
# pm      Prandtl-Meyer           26.37976081

# compute total quantities
T0 = (1 / res["tr"]) * T1
P0 = (1 / res["pr"]) * p1
print("---------")
print(f"P0 = {P0}")
print(f"T0 = {T0}")
# ---------
# P0 = 7.824449066867263 atm
# T0 = 522.0 K

Should a solver not be sufficient for your use case, feel free to explore the code implemented inside each flow's type, maybe you'll find a function that suits your needs.

Please:

• visit the documentation page.
• take a look at the notebooks contained in the examples folder. You can also try this package online with Binder.