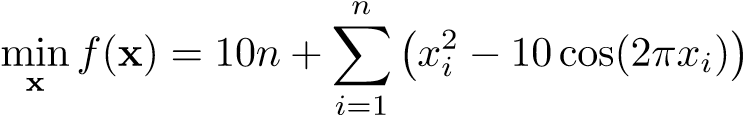geneticAlgorithm

Master's degree subject- Evolutionary Computation - First computer assignment

N-Queens Problem

Given a regular chessboard (NxN dimensions) and N queens, the problem with N-queens is to reallocate them on the chess in a way that no queen may capture another queen. Figure 1 illustrates the capture area of a queen positioned on the board horizontally, vertically or diagonally.

Figure 1: Illustration of an area where one queen can capture another queen in an 8x8 chess

The problem can be formulated as a classical Constraint satisfaction problem, whose goal is to find a configuration of the queens in the board that does not violate any constraints.

In order to solve this problem by using Genetic Algorithms (GA) we must first define:

• a representation (codification) for the individuals (i.e. candidate solution);

• a fitness function to evaluate the performance of a candidate solution;

• one or more genetic variation operator;

• one or more selection mechanism;

• a stop criteria, for example, either generation number or a fitness value.

Some suggestions to be used in the implementation are:

• Representation:

  • Phenotype (f): a configuration of a chessboard with N queens;

  • Genotype (g) or Chromosome: permutation of integers 1*,2,3,...,N*. It means, g = {i1*,i2,...,iN*} denoting a configuration where the k-th column (vector position) contains a queen positioned in the ik-th row, as illustrated in Figures 2 and 3;

For the adopted representation (N integers permutation), the maximum number of checkmate that can occur is q(f) = N(N − 1)*/*2 and the minimum amount is q(f) = 0.

• Operators:

  • Crossover: generate two new candidate solutions from the combination of two parents chromosomes. The generated candidate solutions must be valid permutations.

  • Mutation: randomly selects two positions on a chromosome (permutation) and change the values of these positions.

• Selection:

  • Parents selection: tournament selection.

• Stop criteria: stop when an optimal condition is found, i.e. q(f) = 0, or when a maximum number of generations has been reached.

Figure 2: Phenotype of a candidate solution

Figure 3: Corresponding Genotype to the Phenotype illustrated in the Figure 2

Assignment 1: Implement a GA for the N-queens problem by considering a fixed size 8x8 board. Check with how many generations on average your algorithm is achieving the best solution. Illustrate with graphs and/or tables. In your implementation, you are free to modify or add other forms of selection, crossover and mutation.

Rastrigin Function

The Rastrigin function is a non-convex function used to evaluate the performance of optimization algorithms. It was initially proposed by Rastrigin [1] as a two-dimensional function and later generalized by Muhlenbein et al. [2].

Assignment 2: The goal is to implement a GA and apply it to minimize the Rastrigin function with n =10 variables.

with xi ∈ [−5.12,5.12]. The global minima is x∗ = 0, where f*(x∗) = 0. The GA must have the following characteristics:

1. Representation of the variables using binary codification;

2. Selection operator of individuals by means of:

   • Roulette wheel with 50% of probability;

   • Tournament with 50% of probability.

3. Crossover: 1 cutoff point per variable;

4. Mutation: bit flip;

5. Others operators are free to use.

Define the values of the hyper-parameters pc and pm or make a dynamic adjustment of them. The computational budget is 10,000 fitness function evaluations.

Important note:

• The input and output parameters must be according to the following statements:

[x∗,f∗] = firstname lastname[nvar,ncal], being:

x∗: vector which contains the variables of the best individual; f∗: fitness function evaluated over x∗ ncal: total number of calls (or evaluations) of the fitness function; nvar: number of decision variables.

Submission

• Please submit a Jupyter (Ipython) notebook. Only one notebook should be delivered. Please merge both problems into the same .ipynb file. The notebook has to include all the code (with appropriate comments) necessary to run all the experiments, present the results using text, plots, explanations of what has been done and the interpretation of the results.

• Only the notebook should be submitted. The implementation, the results achieved for both problems and also the organization of the notebook are going to be evaluated. The Teaching Assistant has to be able to reproduce all the experiments simply by running all the notebook cells in order.

• The parameters of both problems must be set so that the entire notebook works normally. Input and output should be presented very explicitly.

References

1. L. A. Rastrigin. Systems of extremal control. Nauka, 1974.

2. H. Mu¨hlenbein, D. Schomisch and J. Born. ”The Parallel Genetic Algorithm as Function Optimizer ”. Parallel Computing, 17, 1991.

3. Agoston E. Eiben, and James E. Smith. Introduction to evolutionary computing. Vol. 53. Berlin: springer, 2003.