La tarea 1 consiste en crear una red neuronal que se alimente de datasets de clasificación y devuelva gráficos de [error, precision] vs epoch y confusion matrix
Para correrlo, use
python run Tarea1.pyy correrá automáticamente, imprimiendo 20 gráficos en pantalla debido a:
- 2 datasets (Iris y Breast Cancer)
- 5 particiones KFold-Cross Validation
- 2 tipos de gráficos ([error, precision] vs epoch y confusion matrix)
Alternativamente, puede usar Run en Pycharm.
Se usaron las librerías:
- numpy para operar datos
- sklearn.metrics para la confusion_matrix
- sklearn.datasets para los datasets load_breast_cancer y load_iris
- sklearn.model_selection para KFold
- matplotlib.pyplot para los gráficos
La red esta implementada con tres clases principales: NeuralNetwork, NeuronLayer y Perceptron, representando cada uno de los elementos de una red neuronal.
Respecto a las dificultades que hubo al hacer la tarea, trabajar con las distintas dimensiones de los elementos y comprender cuando obtener los datos de error y precisión fue motivo de consultas a un auxiliar.
La red es relativamente rápida para datasets pequeños, demorándose en correr la tarea completa alrededor de 5 minutos, con 200 epochs el trabajo sobre Iris, y 100 epochs el trabajo sobre Breast Cancer.
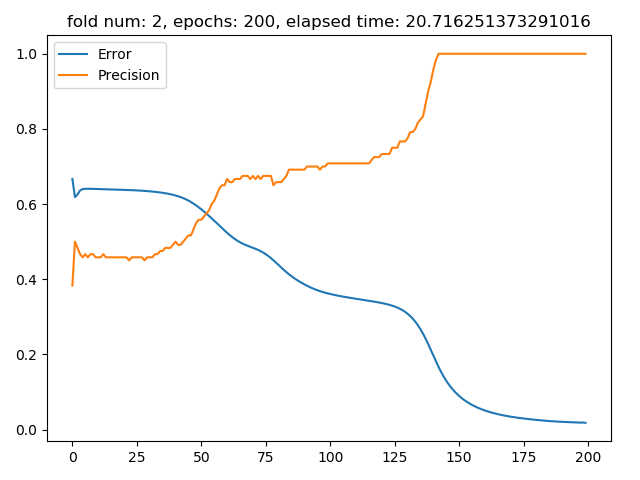
Para que las redes que trabajan con el dataset de iris dieran resultados más acertados, se tuvo que incrementar la cantidad de epochs de 100 a 200, pues entregaba casi siempre resultados erróneos.
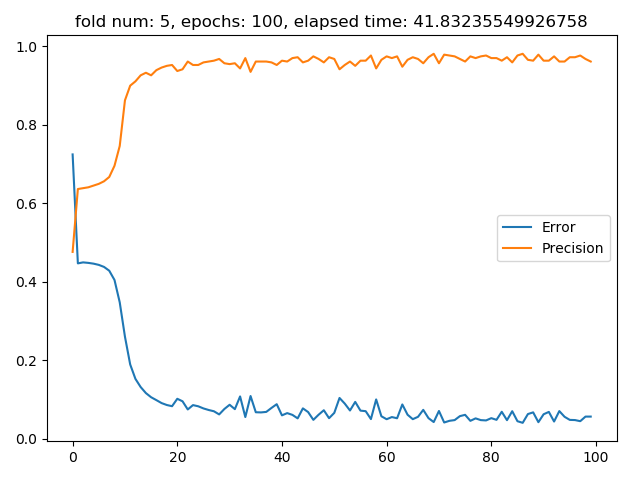
En los gráficos de error y precisión, el eje X representa los epoch sobre los que se entrenó la red, mientras que el eje y representa el valor de precisión (naranjo) o error (azul).
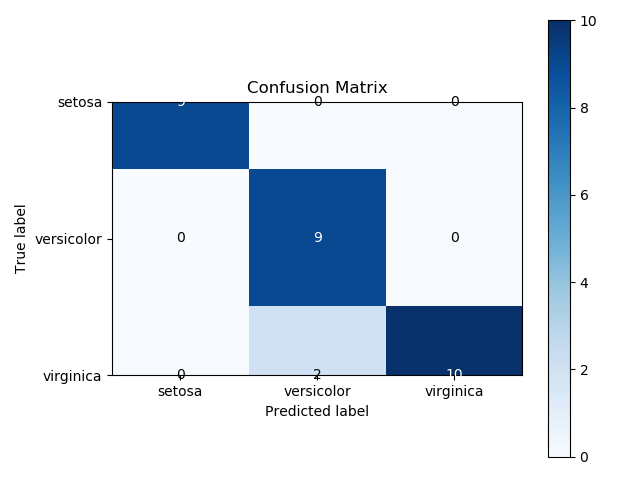
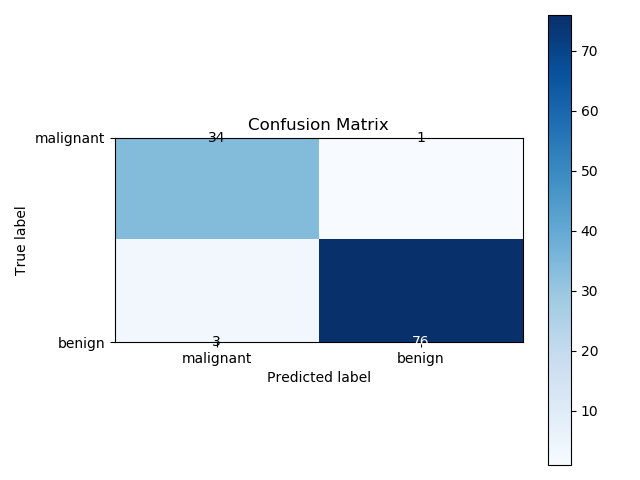
En la matriz de confusión, se muestran los labels trabajados y el reconocimiento que tuvo real.
La red funciona mejor a más epochs se le de para entrenar, para ello al final del archivo Tarea1.py, en las líneas 261 y 266 puede modificar la cantidad de epochs dado.
Breast Cancer Confusion Matrix:
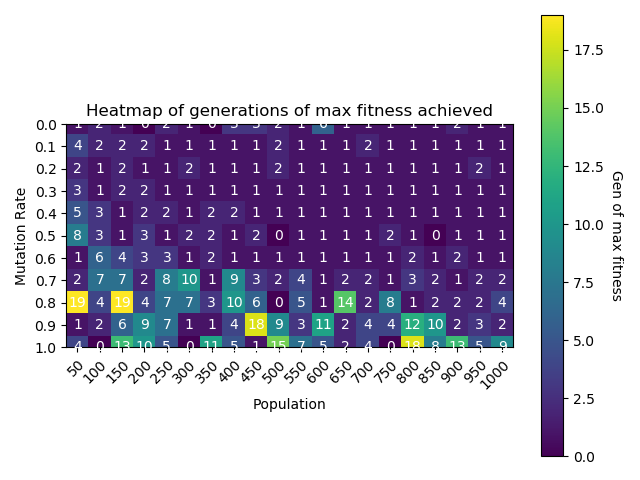
La tarea 2 consiste en crear un algoritmo genético que resuelva un problema a elección (en este caso Unbounded Knapsack) y devuelva un gráfico best, mean y worst fitness por generación (se elige la iteración con indice de mutación 1 y población 1000), y un gráfico heatmap a elección con los ratios de mutación y población dados (en este caso, se eligió la última generación en que aumenta el fitness)
Para correrlo, use
python run Tarea2.pyy correrá automáticamente, imprimiendo 2 gráficos en pantalla debido a:
- Generación de un gen aleatorio, su reproducción y mutación
- Elección de mejor fitness
Alternativamente, puede usar Run en Pycharm.
Se usaron las librerías:
- numpy para operar datos
- matplotlib.pyplot para los gráficos
El algoritmo esta implementado con una clase principal: Genome, representando cada operación principal de un algoritmo genético.
Respecto a las dificultades que hubo al hacer la tarea, trabajar con las distintas dimensiones de los elementos y comprender cuando obtener los datos de fitness para los gráficos fue motivo de consultas a un auxiliar, pues sentí que por un tema de lenguaje no entendí que quizo decir en un inicio.
El algoritmo es relativamente rápido para conjuntos de población pequeños, demorándose en correr la tarea completa alrededor de 3 minutos.
Para algoritmos con mayor población, se demora mucho más, pero encuentra el fitness adecuado en menor cantidad de generaciones. Respecto a la mutación, para indices [0,0.1] U [0.6,1], los fitness de peores casos oscilan mayormente, pues entregaba casi siempre resultados alejados al esperado.
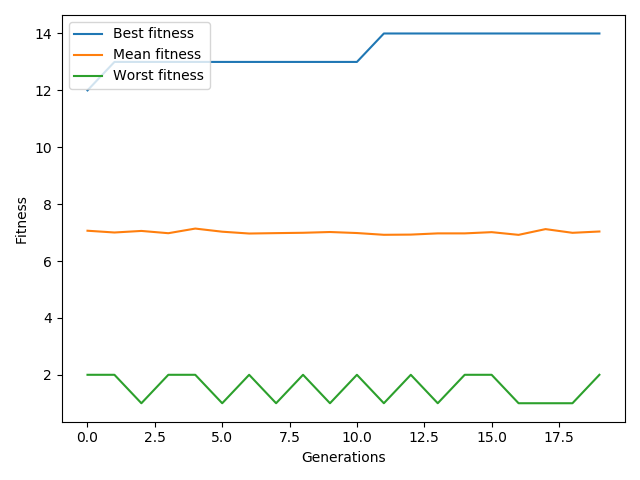
En el gráfico de fitness por generación, el eje X representa cada generación del algoritmo, mientras que el eje Y representa el indice de fitness (en este caso, el óptimo es 36).
En el heatmap, el eje X representa la cantidad de población del genoma, mientras que el eje Y representa los índices de mutación, con cada recuadro la última generación en la que hubo un aumento del fitness.
Los ejercicios 4 y 5 producen los mismos gráficos para los problemas de encontrar un string de bits, y encontrar una palabra.
Una aplicación real de los algoritmos genéticos es encontrar soluciones aproximadas a problemas en que encontrar el óptimo de manera segura sea muy largo o dificil (NP-hard). Un ejemplo clásico sería problemas basado en el vendedor viajero, como enrutamiento de tráfico. En el campo de la robótica, podría usarse para crear robots de aprendizaje que imiten de mejor manera tareas no automatizables.
Fitness por generación en iteración con indice mutación 1 y población 1000, caso ejercicio4:
Heatmap de generación de última subida, indiceMutacion vs cantPoblacion, caso ejercicio4: